The Initial Buret Reading for a Titration Using 0.5345 M of Barium Chloride Was 0.6 Ml.

março 10, 2022 Postar um comentário

Affiliate fourteen. Acrid-Base of operations Equilibria

14.7 Acid-Base of operations Titrations

Learning Objectives

Past the end of this section, you will be able to:

Interpret titration curves for strong and weak acid-base systems
Compute sample pH at important stages of a titration
Explain the office of acid-base of operations indicators

As seen in the chapter on the stoichiometry of chemic reactions, titrations can be used to quantitatively analyze solutions for their acid or base concentrations. In this section, we will explore the changes in the concentrations of the acidic and basic species present in a solution during the process of a titration.

Titration Curve

Previously, when nosotros studied acid-base reactions in solution, nosotros focused only on the signal at which the acid and base were stoichiometrically equivalent. No consideration was given to the pH of the solution before, during, or after the neutralization.

Example 1

Calculating pH for Titration Solutions: Strong Acrid/Strong Base
A titration is carried out for 25.00 mL of 0.100 M HCl (strong acid) with 0.100 M of a strong base NaOH the titration bend is shown in Effigy i. Calculate the pH at these volumes of added base of operations solution:

(a) 0.00 mL

(b) 12.fifty mL

(d) 37.50 mL

Solution
Since HCl is a strong acid, we can assume that all of it dissociates. The initial concentration of H₃O⁺ is [latex][\text{H}_3\text{O}^{+}]_0 = 0.100\;Yard[/latex]. When the base solution is added, information technology also dissociates completely, providing OH⁻ ions. The H₃O⁺ and OH⁻ ions neutralize each other, and then only those of the two that were in excess remain, and their concentration determines the pH. Thus, the solution is initially acidic (pH < 7), but eventually all the hydronium ions present from the original acid are neutralized, and the solution becomes neutral. As more base of operations is added, the solution turns basic.

The total initial corporeality of the hydronium ions is:

[latex]\text{n(H}^{+})_0 = [\text{H}_3\text{O}^{+}]_0\;\times\;0.02500\;\text{L} = 0.002500\;\text{mol}[/latex]

Once Ten mL of the 0.100-M base solution is added, the number of moles of the OH⁻ ions introduced is:

[latex]\text{n(OH}^{-})_0 = 0.100\;M\;\times\;\text{X\;mL}\;\times\;(\frac{ane\;\text{L}}{1000\;\text{mL}})[/latex]

The full book becomes: [latex]V = (25.00\;\text{mL}\;+\;\text{X\;mL})(\frac{1\;\text{L}}{thou\;\text{mL}})[/latex]

The number of moles of H₃O⁺ becomes:

[latex]\text{n(H}^{+}) = \text{n(H}^{+})_0\;-\;\text{due north(OH}^{-})_0 = 0.002500\;\text{mol}\;-\;0.100\;M\;\times\;\text{10\;mL}\;\times\;(\frac{1\;\text{50}}{k\;\text{mL}})[/latex]

The concentration of H_threeO⁺ is:

[latex][\text{H}_3\text{O}^{+}] = \frac{\text{north(H}^{+})}{V} = \frac{0.002500\;\text{mol}\;-\;0.100\;M\;\times\;\text{X\;mL}\;\times\;(\frac{1\;\text{Fifty}}{1000\;\text{mL}})}{(25.00\;\text{mL}\;+\;\text{Ten\;mL})(\frac{1\;\text{Fifty}}{k\;\text{mL}})}[/latex]

[latex]= \frac{0.002500\;\text{mol}\;\times\;(\frac{one thousand\;\text{mL}}{1\;\text{L}})\;-\;0.100\;Grand\;\times\;\text{X\;mL}}{25.00\;\text{mL}\;+\;\text{10\;mL}}[/latex]

[latex]\text{pH} = -\text{log}([\text{H}_3\text{O}^{+}])[/latex]

The preceding calculations work if [latex]\text{northward(H}^{+})_0\;-\;\text{n(OH}^{-})_0\;{\textgreater}\;0[/latex] and and so northward(H⁺) > 0. When [latex]\text{n(H}^{+})_0 = \text{n(OH}^{-})_0[/latex], the H_threeO⁺ ions from the acid and the OH⁻ ions from the base mutually neutralize. At this point, the but hydronium ions left are those from the autoionization of h2o, and in that location are no OH⁻ particles to neutralize them. Therefore, in this case:

[latex][\text{H}_3\text{O}^{+}] = [\text{OH}^{-}]\text{,\;}[\text{H}_3\text{O}^{+}] = K_{\text{due west}} = 1.0\;\times\;10^{-fourteen}\text{;\;}[\text{H}_3\text{O}^{+}] = 1.0\;\times\;x^{-7}[/latex]

[latex]\text{pH} = -\text{log}(one.0\;\times\;10^{-7}) = 7.00[/latex]

Finally, when [latex]\text{n(OH}^{-})_0\;{\textgreater}\;\text{northward(H}^{+})_0[/latex], there are non enough H₃O⁺ ions to neutralize all the OH⁻ ions, and instead of [latex]\text{due north(H}^{+}) = \text{n(H}^{+})_0\;-\;\text{north(OH}^{-})_0[/latex], we calculate: [latex]\text{north(OH}^{-}) = \text{north(OH}^{-})_0\;-\;\text{n(H}^{+})_0[/latex]

In this instance:

[latex][\text{OH}^{-}] = \frac{\text{n(OH}^{-})}{V} = \frac{0.100\;Yard\;\times\;\text{X\;mL}\;\times\;(\frac{1\;\text{50}}{k\;\text{mL}})\;-\;0.002500\;\text{mol}}{(25.00\;\text{mL}\;+\;\text{X\;mL})(\frac{1\;\text{L}}{thousand\;\text{mL}})}[/latex]

[latex]= \frac{0.100\;M\;\times\;\text{X\;mL}\;-\;0.002500\;\text{mol}\;\times\;(\frac{one thousand\;\text{mL}}{1\;\text{Fifty}})}{25.00\;\text{mL}\;+\;\text{10\;mL}}[/latex]

[latex]\text{pH} = 14\;-\;\text{pOH} = 14\;+\;\text{log}([\text{OH}^{-}])[/latex]

Let us now consider the 4 specific cases presented in this problem:

(a) 10 = 0 mL

[latex][\text{H}_3\text{O}^{+}] = \frac{\text{n(H}^{+})}{V} = \frac{0.002500\;\text{mol}\;\times\;(\frac{m\;\text{mL}}{1\;\text{L}})}{25.00\;\text{mL}} = 0.1\;M[/latex]

pH = −log(0.100) = 1.000

(b) X = 12.fifty mL

[latex][\text{H}_3\text{O}^{+}] = \frac{\text{due north(H}^{+})}{V} = \frac{0.002500\;\text{mol}\;\times\;(\frac{thousand\;\text{mL}}{ane\;\text{L}})\;-\;0.100\;Grand\;\times\;12.50\;\text{mL}}{25.00\;\text{mL}\;+\;12.50\;\text{mL}} = 0.0333\;M[/latex]

pH = −log(0.0333) = 1.477

Since the volumes and concentrations of the acrid and base of operations solutions are the same: [latex]\text{due north(H}^{+})_0 = \text{north(OH}^{-})_0[/latex], and pH = 7.000, as described earlier.

(d) 10 = 37.50 mL

In this example:

[latex]\text{n(OH}^{-})_0\;{\textgreater}\;\text{n(H}^{+})_0[/latex]

[latex][\text{OH}^{-}] = \frac{\text{northward(OH}^{-})}{V} = \frac{0.100\;M\;\times\;35.70\;\text{mL}\;-\;0.002500\;\text{mol}\;\times\;(\frac{1000\;\text{mL}}{1\;\text{50}})}{25.00\;\text{mL}\;+\;37.50\;\text{mL}} = 0.0200\;Grand[/latex]

pH = 14 − pOH = 14 + log([OH⁻]) = xiv + log(0.0200) = 12.xxx

Check Your Learning
Calculate the pH for the strong acid/stiff base titration between 50.0 mL of 0.100 K HNO_three(aq) and 0.200 M NaOH (titrant) at the listed volumes of added base: 0.00 mL, 15.0 mL, 25.0 mL, and 40.0 mL.

Answer:

0.00: 1.000; xv.0: one.5111; 25.0: 7; 40.0: 12.523

In the case, we calculated pH at four points during a titration. Table 4 shows a detailed sequence of changes in the pH of a potent acrid and a weak acid in a titration with NaOH.

Volume of 0.100 Yard NaOH Added (mL)	Moles of NaOH Added	pH Values 0.100 M HCl^[1]	pH Values 0.100 Thou CH₃CO₂H^[2]
0.0	0.0	i.00	2.87
5.0	0.00050	1.18	4.xiv
10.0	0.00100	1.37	4.57
15.0	0.00150	ane.60	four.92
20.0	0.00200	1.95	5.35
22.0	0.00220	2.twenty	5.61
24.0	0.00240	2.69	6.13
24.5	0.00245	3.00	6.44
24.nine	0.00249	3.70	7.14
25.0	0.00250	seven.00	viii.72
25.1	0.00251	x.xxx	10.xxx
25.5	0.00255	11.00	11.00
26.0	0.00260	11.29	11.29
28.0	0.00280	11.75	11.75
xxx.0	0.00300	eleven.96	11.96
35.0	0.00350	12.22	12.22
xl.0	0.00400	12.36	12.36
45.0	0.00450	12.46	12.46
50.0	0.00500	12.52	12.52
Table 4. pH Values in the Titrations of a Strong Acid with a Strong Base and of a Weak Acrid with a Stiff Base

The simplest acid-base of operations reactions are those of a strong acid with a strong base of operations. Table 4 shows data for the titration of a 25.0-mL sample of 0.100 Chiliad hydrochloric acid with 0.100 Thou sodium hydroxide. The values of the pH measured later on successive additions of minor amounts of NaOH are listed in the beginning cavalcade of this tabular array, and are graphed in Figure one, in a form that is chosen a titration bend. The pH increases slowly at first, increases rapidly in the heart portion of the curve, and so increases slowly over again. The point of inflection (located at the midpoint of the vertical part of the bend) is the equivalence point for the titration. It indicates when equivalent quantities of acrid and base are present. For the titration of a stiff acid with a strong base, the equivalence betoken occurs at a pH of vii.00 and the points on the titration curve can be calculated using solution stoichiometry (Table four and Figure 1).

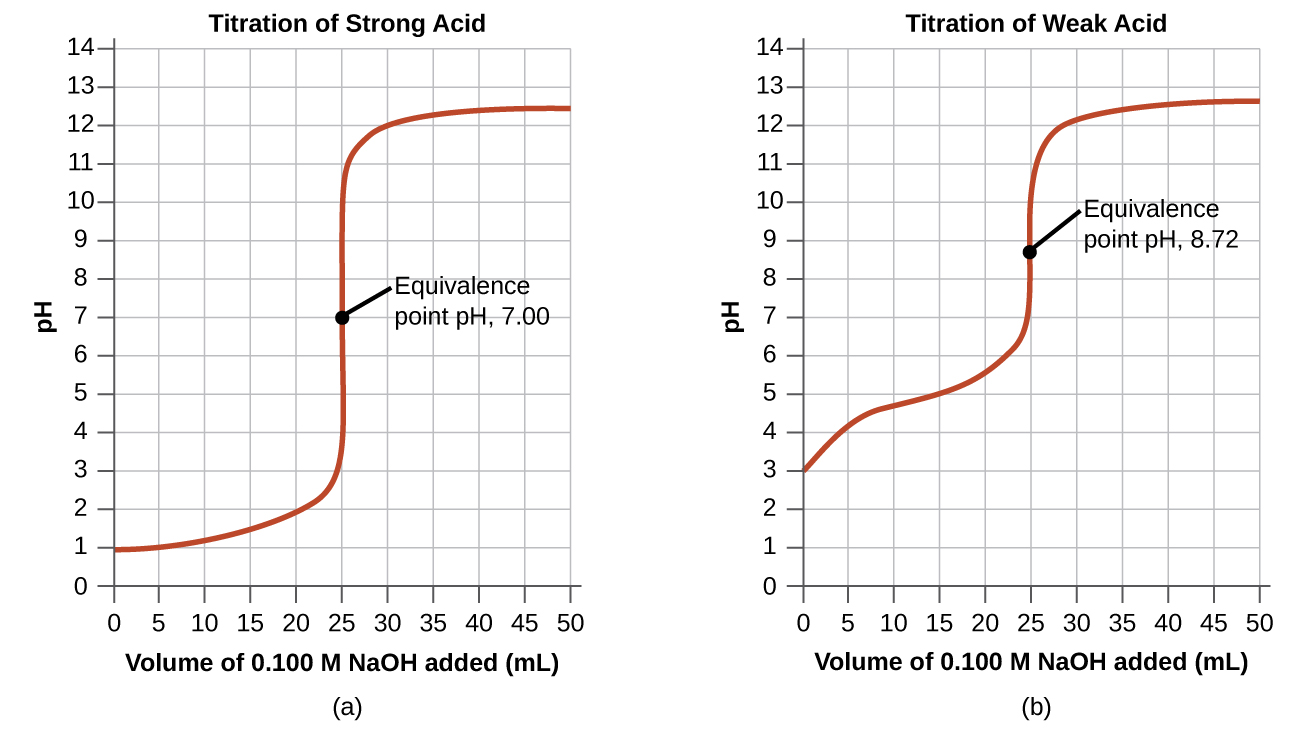
Two graphs are shown. The first graph on the left is titled — **Figure 1.** (a) The titration curve for the titration of 25.00 mL of 0.100 M HCl (potent acid) with 0.100 M NaOH (strong base) has an equivalence bespeak of 7.00 pH. (b) The titration bend for the titration of 25.00 mL of 0.100 M HCl (strong acid) with 0.100 M NaOH (strong base) has an equivalence point of eight.72 pH.

The titration of a weak acid with a strong base (or of a weak base with a strong acid) is somewhat more than complicated than that just discussed, but it follows the aforementioned general principles. Let united states of america consider the titration of 25.0 mL of 0.100 Thou acetic acid (a weak acid) with 0.100 M sodium hydroxide and compare the titration curve with that of the strong acid. Tabular array 4 gives the pH values during the titration, Figure 1 shows the titration curve.

Although the initial volume and molarity of the acids are the same, there are important differences between the two titration curves. The titration curve for the weak acrid begins at a higher value (less acidic) and maintains higher pH values up to the equivalence bespeak. This is considering acerb acrid is a weak acid, which is only partially ionized. The pH at the equivalence point is also higher (eight.72 rather than 7.00) due to the hydrolysis of acetate, a weak base that raises the pH:

[latex]\text{CH}_3\text{CO}_2^{\;\;-}(aq)\;+\;\text{H}_2\text{O}(l)\;{\leftrightharpoons}\;\text{CH}_3\text{CO}_2\text{H}(l)\;+\;\text{OH}^{-}(aq)[/latex]

After the equivalence point, the two curves are identical considering the pH is dependent on the backlog of hydroxide ion in both cases.

Case 2

Titration of a Weak Acid with a Potent Base
The titration bend shown in Figure 3 is for the titration of 25.00 mL of 0.100 M CH₃CO₂H with 0.100 Thousand NaOH. The reaction can be represented as:

[latex]\text{CH}_3\text{CO}_2\text{H}\;+\;\text{OH}^{-}\;{\longrightarrow}\;\text{CH}_3\text{CO}_2^{\;\;-}\;+\;\text{H}_2\text{O}[/latex]

(a) What is the initial pH before any amount of the NaOH solution has been added? One thousand _a = 1.8 × 10⁻⁵ for CH_iiiCO_iiH.

(b) Discover the pH after 25.00 mL of the NaOH solution have been added.

(d) Observe the pH after 37.50 mL of the NaOH solution has been added.

Solution
(a) Assuming that the dissociated amount is small compared to 0.100 Thousand, we discover that:

[latex]K_{\text{a}} = \frac{[\text{H}_3\text{O}^{+}][\text{CH}_3\text{CO}_2^{\;\;-}]}{[\text{CH}_3\text{CO}_2\text{H}]}\;{\approx}\;\frac{[\text{H}_3\text{O}^{+}]^ii}{[\text{CH}_3\text{CO}_2\text{H}]_0}[/latex], and [latex][\text{H}_3\text{O}^{+}] = \sqrt{K_{\text{a}}\;\times\;[\text{CH}_3\text{CO}_2\text{H}]} = \sqrt{1.8\;\times\;x^{-5}\;\times\;0.100} = ane.3\;\times\;10^{-3}[/latex]

[latex]\text{pH} = -\text{log}(i.iii\;\times\;10^{-iii}) = 2.87[/latex]

(b) After 25.00 mL of NaOH are added, the number of moles of NaOH and CH₃CO₂H are equal because the amounts of the solutions and their concentrations are the same. All of the CH_threeCO_twoH has been converted to [latex]\text{CH}_3\text{CO}_2^{\;\;-}[/latex]. The concentration of the [latex]\text{CH}_3\text{CO}_2^{\;\;-}[/latex] ion is:

[latex]\frac{0.00250\;\text{mol}}{0.0500\;\text{50}} = 0.0500\;M\;\text{CH}_3\text{CO}_2^{\;\;-}[/latex]

The equilibrium that must be focused on at present is the basicity equilibrium for [latex]\text{CH}_3\text{CO}_2^{\;\;-}[/latex]:

[latex]\text{CH}_3\text{CO}_2^{\;\;-}(aq)\;+\;\text{H}_2\text{O}(fifty)\;{\rightleftharpoons}\;\text{CH}_3\text{CO}_2\text{H}(aq)\;+\;\text{OH}^{-}(aq)[/latex]

then we must make up one's mind One thousand _b for the base past using the ion product constant for water:

[latex]K_{\text{b}} = \frac{[\text{CH}_3\text{CO}_2\text{H}][\text{OH}^{-}]}{[\text{CH}_3\text{CO}_2^{\;\;-}]}[/latex]

[latex]K_{\text{a}} = \frac{[\text{CH}_3\text{CO}_2^{\;\;-}][\text{H}^{+}]}{[\text{CH}_3\text{CO}_2\text{H}]}\text{,\;and so\;}\frac{[\text{CH}_3\text{CO}_2\text{H}]}{[\text{CH}_3\text{CO}_2^{\;\;-}]} = \frac{[\text{H}^{+}]}{K_{\text{a}}}[/latex].

Since Chiliad _w = [H⁺][OH⁻]:

[latex]K_{\text{b}} = \frac{[\text{H}^{+}][\text{OH}^{-}]}{K_{\text{a}}} = \frac{K_{\text{w}}}{K_{\text{a}}} = \frac{1.0\;\times\;10^{-14}}{1.8\;\times\;10^{-v}} = five.6\;\times\;ten^{-10}[/latex]

Let us denote the concentration of each of the products of this reaction, CH₃CO₂H and OH⁻, every bit x. Using the assumption that x is small compared to 0.0500 M, [latex]K_{\text{b}} = \frac{x^{2}}{0.0500\;Chiliad}[/latex], and and then:

[latex]ten = [\text{OH}^{-}] = 5.3\;\times\;10^{-6}[/latex]

[latex]\text{pOH} = -\text{log}(5.3\;\times\;10^{-half-dozen}) = 5.28[/latex]

[latex]\text{pH} = 14.00\;-\;5.28 = 8.72[/latex]

Note that the pH at the equivalence signal of this titration is significantly greater than 7.

(c) In (a), 25.00 mL of the NaOH solution was added, and and then practically all the CH_threeCO_iiH was converted into [latex]\text{CH}_3\text{CO}_2^{\;\;-}[/latex]. In this case, only 12.50 mL of the base solution has been introduced, and so merely half of all the CH₃CO₂H is converted into [latex]\text{CH}_3\text{CO}_2^{\;\;-}[/latex]. The total initial number of moles of CH_threeCO₂H is 0.02500L × 0.100 M = 0.00250 mol, and and then after adding the NaOH, the numbers of moles of CH_threeCO₂H and [latex]\text{CH}_3\text{CO}_2^{\;\;-}[/latex] are both approximately equal to [latex]\frac{0.00250\;\text{mol}}{2} = 0.00125\;\text{mol}[/latex], and their concentrations are the aforementioned.

Since the amount of the added base is smaller than the original corporeality of the acrid, the equivalence point has not been reached, the solution remains a buffer, and we can use the Henderson-Hasselbalch equation:

[latex]\text{pH} = \text{p}K_{\text{a}}\;+\;\text{log}\frac{[\text{Base}]}{[\text{Acid}]} = -\text{log}(K_{\text{a}})\;+\;\text{log}\frac{[\text{CH}_3\text{CO}_2^{\;\;-}]}{[\text{CH}_3\text{CO}_2\text{H}]} = -\text{log}(1.8\;\times\;ten^{-5})\;+\;\text{log}(1)[/latex]

(as the concentrations of [latex]\text{CH}_3\text{CO}_2^{\;\;-}[/latex] and CH_threeCO₂H are the same)

Thus:

[latex]\text{pH} = -\text{log}(1.viii\;\times\;10^{-five}) = 4.74[/latex]

(the pH = the pG _a at the halfway signal in a titration of a weak acid)

(d) Afterwards 37.l mL of NaOH is added, the amount of NaOH is 0.03750 L × 0.100 M = 0.003750 mol NaOH. Since this is past the equivalence point, the excess hydroxide ions will make the solution basic, and we tin again use stoichiometric calculations to determine the pH:

[latex][\text{OH}^{-}] = \frac{(0.003750\;\text{mol}\;-\;0.00250\;\text{mol})}{0.06250\;\text{L}} = 2.00\;\times\;10^{-2}\;G[/latex]

Then:

[latex]\text{pOH} = -\text{log}(2.00\;\times\;ten^{-ii}) = 1.70\text{,\;and\;pH} = fourteen.00\;-\;i.70 = 12.30[/latex]

Note that this outcome is the same equally for the strong acrid-strong base of operations titration example provided, since the amount of the potent base added moves the solution by the equivalence point.

Cheque Your Learning
Calculate the pH for the weak acid/strong base titration between 50.0 mL of 0.100 M HCOOH(aq) (formic acid) and 0.200 M NaOH (titrant) at the listed volumes of added base of operations: 0.00 mL, 15.0 mL, 25.0 mL, and 30.0 mL.

Reply:

0.00 mL: 2.37; 15.0 mL: three.92; 25.00 mL: 8.29; xxx.0 mL: 12.097

Acid-Base Indicators

Certain organic substances alter colour in dilute solution when the hydronium ion concentration reaches a particular value. For example, phenolphthalein is a colorless substance in any aqueous solution with a hydronium ion concentration greater than 5.0 × 10^−nine 1000 (pH < 8.3). In more than bones solutions where the hydronium ion concentration is less than 5.0 × 10⁻⁹ Thousand (pH > 8.3), it is red or pink. Substances such as phenolphthalein, which tin be used to determine the pH of a solution, are chosen acid-base of operations indicators. Acrid-base indicators are either weak organic acids or weak organic bases.

The equilibrium in a solution of the acrid-base indicator methyl orangish, a weak acid, tin be represented by an equation in which nosotros use HIn equally a simple representation for the complex methyl orangish molecule:

[latex]\begin{array}{ccccccc} \text{HIn}(aq) & + & \text{H}_2\text{O}(50) & {\leftrightharpoons} & \text{H}_3\text{O}^{+}(aq) & + & \text{In}^{-}(aq) \\[0.5em] \text{red} & & & & & & \text{yellow} \end{array}[/latex]

[latex]K_{\text{a}} = \frac{[\text{H}_3\text{O}^{+}][\text{In}^{-}]}{[\text{HIn}]} = 4.0\;\times\;10^{-iv}[/latex]

The anion of methyl orange, In⁻, is yellow, and the nonionized grade, HIn, is red. When we add acid to a solution of methyl orangish, the increased hydronium ion concentration shifts the equilibrium toward the nonionized red course, in accord with Le Châtelier's principle. If we add base, we shift the equilibrium towards the xanthous course. This behavior is completely analogous to the action of buffers.

An indicator'southward color is the visible issue of the ratio of the concentrations of the 2 species In⁻ and HIn. If most of the indicator (typically almost 60−xc% or more) is present every bit In⁻, then nosotros encounter the color of the In⁻ ion, which would be xanthous for methyl orangish. If most is present as HIn, then nosotros see the color of the HIn molecule: ruddy for methyl orange. For methyl orange, nosotros can rearrange the equation for K _a and write:

[latex]\frac{[\text{In}^{-}]}{[\text{HIn}]} = \frac{[\text{substance\;with\;xanthous\;color}]}{[\text{substance\;with\;ruby-red\;color}]} = \frac{K_{\text{a}}}{[\text{H}_3\text{O}^{+}]}[/latex]

This shows us how the ratio of [latex]\frac{[\text{In}^{-}]}{[\text{HIn}]}[/latex] varies with the concentration of hydronium ion.

The above expression describing the indicator equilibrium can be rearranged:

[latex]\frac{[\text{H}_3\text{O}^{+}]}{K_{\text{a}}} = \frac{[\text{HIn}]}{[\text{In}^{-}]}[/latex]

[latex]\text{log}(\frac{[\text{H}_3\text{O}^{+}]}{K_{\text{a}}}) = \text{log}(\frac{[\text{HIn}]}{[\text{In}^{-}]})[/latex]

[latex]\text{log}([\text{H}_3\text{O}^{+}])\;-\;\text{log}(K_{\text{a}}) = -\text{log}(\frac{[\text{In}^{-}]}{[\text{HIn}]})[/latex]

[latex]-\text{pH}\;+\;\text{p}K_{\text{a}} = -\text{log}(\frac{[\text{In}^{-}]}{[\text{HIn}]})[/latex]

[latex]\text{pH} = \text{p}K_{\text{a}}\;+\;\text{log}(\frac{[\text{In}^{-}]}{[\text{HIn}]})\;\text{or\;pH} = \text{p}K_{\text{a}}\;+\;\text{log}(\frac{[\text{base of operations}]}{[\text{acid}]})[/latex]

The concluding formula is the aforementioned as the Henderson-Hasselbalch equation, which can be used to describe the equilibrium of indicators.

When [H₃O⁺] has the same numerical value as Thousand _a, the ratio of [In⁻] to [HIn] is equal to 1, meaning that 50% of the indicator is present in the red form (HIn) and l% is in the yellow ionic form (In⁻), and the solution appears orange in color. When the hydronium ion concentration increases to viii × 10⁻⁴ M (a pH of three.1), the solution turns red. No change in color is visible for any further increment in the hydronium ion concentration (decrease in pH). At a hydronium ion concentration of 4 × 10^−v M (a pH of 4.iv), virtually of the indicator is in the yellowish ionic form, and a farther decrease in the hydronium ion concentration (increase in pH) does non produce a visible colour change. The pH range betwixt 3.1 (blood-red) and 4.four (yellow) is the color-alter interval of methyl orange; the pronounced color change takes identify between these pH values.

There are many different acid-base of operations indicators that cover a wide range of pH values and can be used to make up one's mind the judge pH of an unknown solution by a process of elimination. Universal indicators and pH paper contain a mixture of indicators and showroom different colors at unlike pHs. Figure 2 presents several indicators, their colors, and their color-alter intervals.

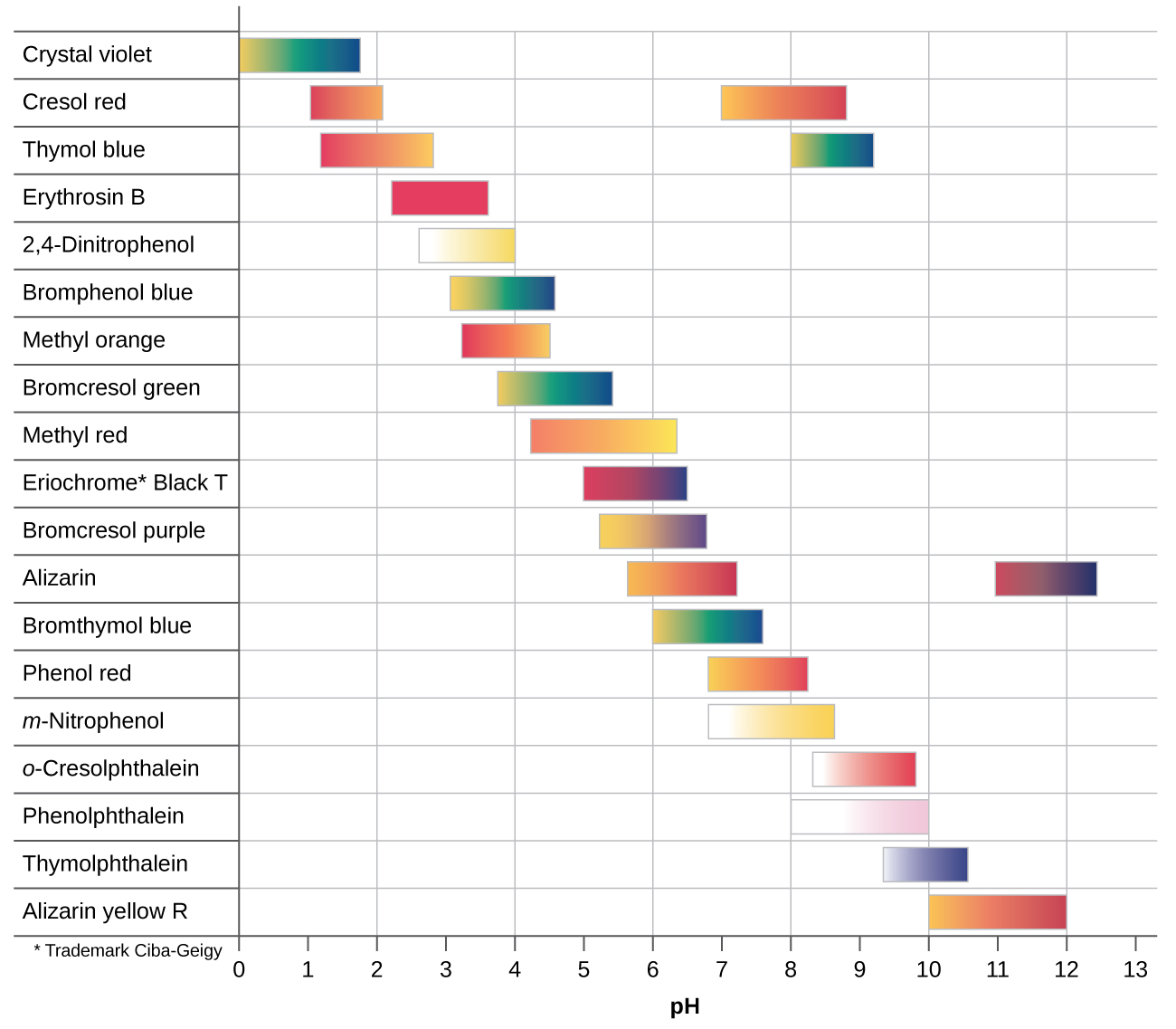
This figure provides a graphical representation of indicators and color ranges. A horizontal axis is labeled — **Figure 2.** This chart illustrates the ranges of color change for several acid-base of operations indicators.

Titration curves help us choice an indicator that will provide a sharp colour modify at the equivalence point. The best choice would be an indicator that has a color change interval that brackets the pH at the equivalence point of the titration.

The color alter intervals of three indicators are shown in Figure three. The equivalence points of both the titration of the strong acid and of the weak acrid are located in the color-change interval of phenolphthalein. Nosotros can use it for titrations of either strong acid with strong base of operations or weak acid with strong base of operations.

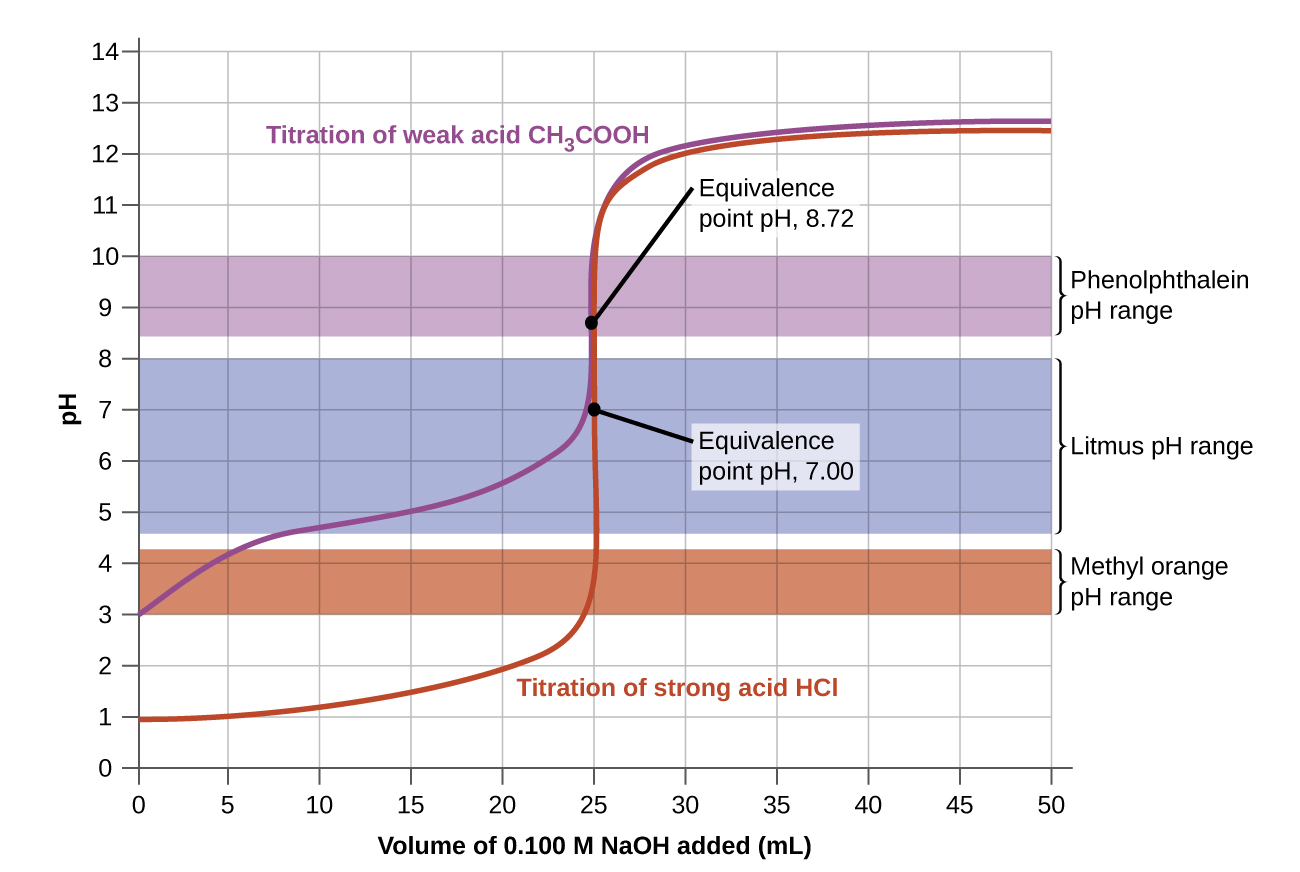
A graph is shown which is titled — **Figure 3.** The graph shows a titration curve for the titration of 25.00 mL of 0.100 *Thou* CH₃CO_twoH (weak acid) with 0.100 M NaOH (strong base) and the titration curve for the titration of HCl (strong acid) with NaOH (potent base). The pH ranges for the colour alter of phenolphthalein, litmus, and methyl orange are indicated past the shaded areas.

Litmus is a suitable indicator for the HCl titration because its color change brackets the equivalence point. Withal, we should not use litmus for the CH₃CO_twoH titration considering the pH is inside the color-change interval of litmus when only almost 12 mL of NaOH has been added, and information technology does not leave the range until 25 mL has been added. The color change would be very gradual, taking place during the add-on of xiii mL of NaOH, making litmus useless equally an indicator of the equivalence signal.

We could employ methyl orange for the HCl titration, but information technology would not give very accurate results: (1) It completes its color alter slightly before the equivalence point is reached (but very shut to information technology, and then this is not too serious); (two) it changes color, as Figure 3 shows, during the improver of nearly 0.v mL of NaOH, which is not so abrupt a color change as that of litmus or phenolphthalein; and (three) it goes from yellow to orange to scarlet, making detection of a precise endpoint much more challenging than the colorless to pink modify of phenolphthalein. Figure 3 shows u.s.a. that methyl orange would exist completely useless as an indicator for the CH₃CO₂H titration. Its color change begins after about one mL of NaOH has been added and ends when about 8 mL has been added. The color alter is completed long earlier the equivalence point (which occurs when 25.0 mL of NaOH has been added) is reached and hence provides no indication of the equivalence point.

Nosotros base our pick of indicator on a calculated pH, the pH at the equivalence point. At the equivalence point, equimolar amounts of acrid and base take been mixed, and the calculation becomes that of the pH of a solution of the salt resulting from the titration.

Key Concepts and Summary

A titration curve is a graph that relates the modify in pH of an acidic or bones solution to the volume of added titrant. The characteristics of the titration curve are dependent on the specific solutions existence titrated. The pH of the solution at the equivalence point may be greater than, equal to, or less than 7.00. The choice of an indicator for a given titration depends on the expected pH at the equivalence betoken of the titration, and the range of the color change of the indicator.

Chemical science End of Chapter Exercises

Explain how to choose the appropriate acid-base indicator for the titration of a weak base with a stiff acid.
Explain why an acrid-base indicator changes color over a range of pH values rather than at a specific pH.
Why can nosotros ignore the contribution of h2o to the concentrations of H_iiiO⁺ in the solutions of following acids:
0.0092 G HClO, a weak acrid

0.0810 M HCN, a weak acid

0.120 Thousand [latex]\text{Atomic number 26(H}_2\text{O})_6^{\;\;2+}[/latex] a weak acid, Thousand _a = i.6 × 10⁻⁷

just not the contribution of water to the concentration of OH⁻?
Nosotros tin can ignore the contribution of h2o to the concentration of OH⁻ in a solution of the following bases:
0.0784 M C₆H_fiveNH_two, a weak base

0.11 Yard (CH₃)₃N, a weak base

just not the contribution of water to the concentration of H₃O⁺?
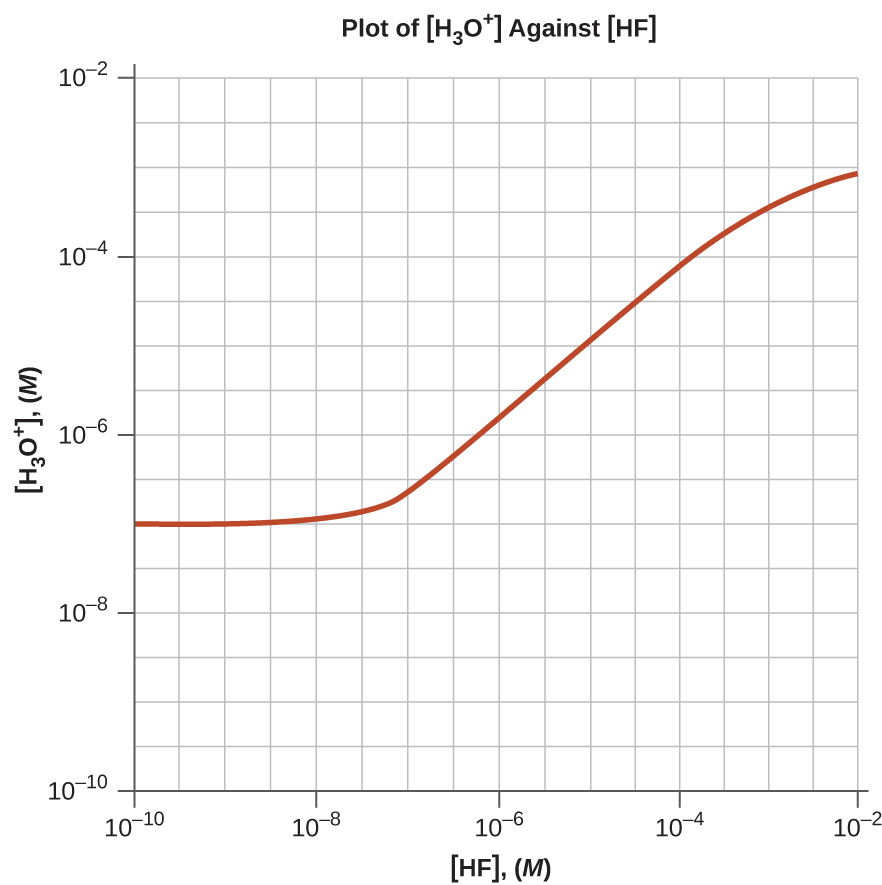
Draw a bend for a series of solutions of HF. Plot [H₃O⁺]_total on the vertical centrality and the full concentration of HF (the sum of the concentrations of both the ionized and nonionized HF molecules) on the horizontal axis. Allow the total concentration of HF vary from i × ten⁻¹⁰ Thousand to one × x^−two Chiliad.
Draw a bend similar to that shown in Effigy 3 for a serial of solutions of NH₃. Plot [OH⁻] on the vertical centrality and the full concentration of NH₃ (both ionized and nonionized NH_iii molecules) on the horizontal centrality. Let the total concentration of NH₃ vary from 1 × ten⁻¹⁰ G to 1 × 10⁻ⁱⁱ Thou.
Calculate the pH at the post-obit points in a titration of twoscore mL (0.040 L) of 0.100 M barbituric acid (K _a = 9.8 × 10⁻⁵) with 0.100 Thousand KOH.
(a) no KOH added

(b) xx mL of KOH solution added

(c) 39 mL of KOH solution added

(d) 40 mL of KOH solution added

(e) 41 mL of KOH solution added
The indicator dinitrophenol is an acid with a Thou _a of i.one × 10⁻⁴. In a 1.0 × 10^−iv–M solution, it is colorless in acrid and yellow in base. Calculate the pH range over which information technology goes from 10% ionized (colorless) to 90% ionized (yellow).

Glossary

acid-base of operations indicator: organic acid or base whose color changes depending on the pH of the solution information technology is in

color-modify interval: range in pH over which the color change of an indicator takes place

titration curve: plot of the pH of a solution of acid or base versus the volume of base of operations or acid added during a titration

Solutions

Answers to Chemistry Cease of Chapter Exercises

1. At the equivalence point in the titration of a weak base with a potent acrid, the resulting solution is slightly acidic due to the presence of the conjugate acid. Thus, pick an indicator that changes color in the acidic range and brackets the pH at the equivalence bespeak. Methyl orange is a good instance.

3. In an acid solution, the only source of OH⁻ ions is water. We use K_w to summate the concentration. If the contribution from h2o was neglected, the concentration of OH⁻ would exist zero.

5.
A graph is shown that is titled